有趣的流体小知识（一）——只凭观察，如何快速估计出湖的深度？

风拂湖面，波光粼粼，美轮美奂。

现在思考这样一个看似不可能的问题：我们只凭观察，没有测量，如何快速估计出湖的深度？

流体动力学告诉我们，在一定条件下，通过观察湖面波浪的行进速度，就可以快速估计水深！

是不是很神奇？生活小技巧 Get！

下面我将从基本流体力学方程出发，给出详细的理论推导过程 ~

公式预警，不感兴趣的小伙伴们也可以跳转最后的答案揭晓环节，直接查看答案！

理论推导环节

如图 1 所示，简化湖面为二维情形，建立平面直角坐标系 $ (z, \,x) $。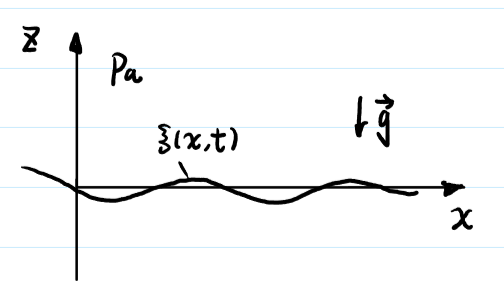

图 1 对湖面水波建立平面直角坐标系

对于湖水，考虑 无粘、不可压、原始静止、小扰动 情况下的 Navier-Stokes (N-S) 方程，即 Euler 方程 \[ \frac{\partial \vec{u}}{\partial t} + \left(\vec{u} \cdot \nabla\right) \vec{u} = - \frac{1}{\rho} \nabla p + \vec{g} \tag{1} \label{eq1} \] 其中，$ \vec{u} $ 为速度，$ \rho $ 为密度，$ p $ 为压强，$ \vec{g} $ 为重力加速度矢量。

由原始静止、小扰动条件，可假设扰动速度与压强为 \[ \vec{u} = \vec{u}_{0} + \vec{u}^{\prime} = \vec{u}^{\prime} , \quad p = p_{0} + p^{\prime} \tag{2} \label{eq2} \] 其中，满足 $ \vec{u} $ 为趋于零的小量，且 $ p^{\prime} \ll p_{0} $。

将式 \(\eqref{eq2}\) 代入式 \(\eqref{eq1}\) ，忽略高阶小对流项 $ \left(\vec{u} \cdot \nabla\right) \vec{u} $ ，得到 线性化 Euler 方程 \[ \frac{\partial \vec{u}^{\prime}}{\partial t} = - \frac{1}{\rho} \nabla p + \vec{g} \tag{3} \label{eq3} \] 首先对上式两边取旋度，由于重力有势，故有 $$ \frac{\partial \vec{\omega}^{\prime}}{\partial t} \equiv 0 \tag{4} \label{eq4} $$ 其中 $ \vec{\omega}^{\prime} = \nabla \times \vec{u}^{\prime} $ 为扰动速度旋度，故扰动速度无旋。 由无旋场与有势场的等价性，可引入扰动速度势 $ \varphi $，满足 $$ \vec{u}^{\prime} = \nabla \varphi \tag{5} \label{eq5} $$ 将上式代入不可压连续性方程 $ \nabla \cdot \vec{u}^{\prime} = 0 $，可得 $$ \nabla^{2} \varphi = \Delta \varphi = \frac{\partial^{2} \varphi}{\partial z^{2}} + \frac{\partial^{2} \varphi}{\partial x^{2}} = 0 \tag{6} \label{eq6} $$

即扰动速度势满足 Laplace 方程。又将式 \(\eqref{eq5}\) 代入式 \(\eqref{eq3}\) 左式，可得 \[ \frac{\partial}{\partial t} \nabla \varphi = - \nabla \left(\frac{p}{\rho} + g z\right) \tag{7} \label{eq7} \] 其中，$ z $ 为水深。另外，由流体静力学知识，有 $$ p = p_{a} - \rho g z + p^{\prime} \tag{8} \label{eq8} $$ 其中，$ p_{a} $ 为湖面上方大气压强，假设保持恒定。将式 $\eqref{eq8}$ 代入式 $\eqref{eq7}$，可得 $$ \frac{\partial}{\partial t} \nabla \varphi = - \nabla \left(\frac{p}{\rho} + g z\right) = - \nabla \left(\frac{p_{a} + p^{\prime}}{\rho}\right) = - \nabla \left(\frac{p^{\prime}}{\rho}\right) \tag{9} \label{eq9} $$ 上式可进一步化为 $$ \frac{\partial \varphi}{\partial t} = - \frac{p^{\prime}}{\rho} \tag{10} \label{eq10} $$ 假设水波自由面方程为 $ z = \zeta \left(x, t\right) $，$ \zeta $ 为偏离平衡位置的位移小量，在该界面上满足 $ p = p_{a} $，代入式 $\eqref{eq8}$ 可得 $$ p^{\prime} = \rho g \zeta \tag{11} \label{eq11} $$

将式 \(\eqref{eq11}\) 代入式 \(\eqref{eq10}\) 可得水波的 动力学边界条件 \[ \left.\frac{\partial \varphi}{\partial t}\right|_{z=\zeta}=-g \zeta \tag{12} \label{eq12} \] 另外，考虑水波自由面作为物质面的运动过程 \[ V_{z} = \left.\frac{\partial \varphi}{\partial z}\right|_{z=\zeta}=\frac{\mathrm{d} \zeta}{\mathrm{d} t} = \frac{\partial \zeta}{\partial t}+\frac{\partial \zeta}{\partial x} \frac{\mathrm{d} x}{\mathrm{d} t} = \frac{\partial \zeta}{\partial t}+\frac{\partial \zeta}{\partial x} u^{\prime} \tag{13} \label{eq13} \] 对上式略去高阶小量，进行线性化，得到水波的 运动学边界条件 \[ \left.\frac{\partial \varphi}{\partial z}\right|_{z=\zeta}=\frac{\partial \zeta}{\partial t} \tag{14} \label{eq14} \] 结合式 \(\eqref{eq12}\) 与 \(\eqref{eq14}\)，可得 \[ \left.\left(\frac{\partial^{2} \varphi}{\partial t^{2}}+g \frac{\partial \varphi}{\partial z}\right)\right|_{z = \zeta} = 0 \tag{15} \label{eq15} \] 下面应用两个边界条件，再通过引入壁面边界条件，求解扰动速度势满足的 Laplace 方程。

引入波长为 $ \lambda $，周期为 $ T $，波数为 $ k = \frac{2 \pi}{\lambda} $，频率为 $ \omega = \frac{2 \pi}{T} $，波速为 $ c = \frac{\omega}{k} = \frac{\lambda}{T} $ 的扰动速度势主模态 (Normal mode) \[ \varphi=\Phi(z) e^{i(k x-\omega t)} \tag{16} \label{eq16} \] 其满足 Laplace 方程 \(\eqref{eq6}\) 的通解为 \[ \Phi(z)=\phi_{1} e^{k z}+\phi_{2} e^{-k z} \tag{17} \label{eq17} \] 其中，$ \phi_{1}, \, \phi_{2} $ 为常数。

• 考虑有限水深情况，水深 $ h $。

图 2 有限水深几何坐标系示意图

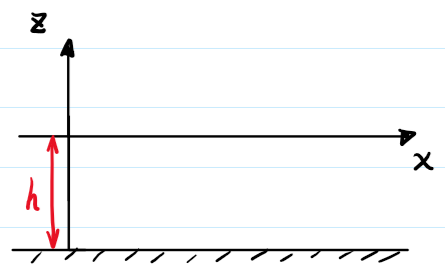
如图 2 所示，考虑水底无穿透边界条件为 \[ \left.\frac{\partial \varphi}{\partial z}\right|_{z = - h} = 0 \tag{18} \label{eq18} \] 将式 \(\eqref{eq16}\) \(\eqref{eq17}\) 代入上式，可令 \[ \phi_{1} e^{-k h}=\phi_{2} e^{k h}=\frac{1}{2} \phi_{0} \tag{19} \label{eq19} \] 进一步可得 \[ \Phi(z)=\phi_{0} \cosh \left[k(z+h)\right] \tag{20} \label{eq20} \] 故扰动速度势 $ \varphi $ 解为 \[ \varphi=\phi_{0} \cosh \left[k(z+h)\right] e^{i(k x-\omega t)} \tag{21} \label{eq21} \] 将上式解代入式 \(\eqref{eq15}\)，可得水波色散关系式 \[ \omega^{2} = gk \tanh (kh) \tag{22} \label{eq22} \] 注意到，当 $ kh \ll 1 $，即 $ h \ll \frac{1}{k} = \frac{\lambda}{2 \pi} $ 时，有 \[ \tanh (kh) = kh - \frac{1}{3} (kh)^{3} + O((kh)^{5}) \approx kh \tag{23} \label{eq23} \] 将上式代入式 \(\eqref{eq22}\)，可得 \[ \omega^{2} = gk \left[kh - \frac{1}{3} (kh)^{3} + O((kh)^{5})\right] = g h k^{2} \left[1 - \frac{1}{3} (k h)^{2} + O ((kh)^{4})\right] \tag{24} \label{eq24} \] 故水波波速 $ c $ 为 \[ c = \frac{\omega}{k} = \frac{\lambda}{T} = \sqrt{g h \left[1 - \frac{1}{3} (k h)^{2} + O ((kh)^{4})\right]} \approx \sqrt{g h} \tag{25} \label{eq25} \] 观察上式可得，若水深 $ h $ 远小于波长 $ \lambda $ 时，此时称该界面波为浅水波，具有非色散特性，特征是波速 \(c\) 仅与以及水深 $ h $ 有关。

答案揭晓环节

有了上面的波速关系式，我们就可以回到最初的问题，即如何仅通过观察波浪行进速度就能估计出湖的深度？

若我们观察到一列行进速度较为稳定的大波浪，其波长 $ \lambda $ 很长，可近似满足远大于水深 $ h $ 的条件，即浅水波，即可快速估计水深 \[ h = \frac{c^{2}}{g} \tag{26} \label{eq26} \] 其中，$ c $ 为水波行进速度， $ g \approx 9.81 \, \text{m} / \text{s}^{2} $ 为重力加速度。

事实上，该关系式在 $ \frac{\lambda}{20} < h < \frac{\lambda}{2} $ 情况下均适用。当然，这只是根据水波动力学推导出的理论关系式，其中包含众多假设条件，实际上只是一种粗略的估计。

最后，值得注意的是，若满足水波波长 $ \lambda $较短，水深 $ h $ 较大，即 $ h > \frac{\lambda}{2} $ 时，通常认为该水波为深水波（或表面波），此时界面波为负色散波，其色散关系式为 \[ c = \sqrt{\frac{g}{k}} \tag{27} \label{eq27} \] 即波长越长，波数越小，波速越大。此时波速与水深无关，这也就意味着我们也就不能根据波速来估计湖的水深啦~

想象一下，站在湖面，欣赏美景，观看浪潮，顺便还能估算出湖的深度，是不是非常神奇呢？（手动狗头 doge）

参考资料

以上就是本期全部内容，参考朱克勤、彭杰老师的《高等流体力学》。

公式推导不够细致，排版也不够美观，还请大家谅解。如有疑问，敬请大家批评指正！

相应文章也发布在我的B站空间专栏上。后续我会不定期更新本博客与专栏，也正在构思相似内容的科普短视频创作，欢迎大家关注！

---

^_^ This is the END of the article. Thank you for reading!

If you think this article is helpful to you, do not hesitate to leave your comments!

Finished by pkufzh (Small Shrimp) on 2022/02/07 .

Who am I? A happy shrimp from Peking University!