有趣的航空航天小知识（一）——探测器绕天体运行轨道方程推导

在经典牛顿力学框架下，给出在有心力下探测器绕天体运行轨道方程推导的一种思路~

假设一个探测器质量为 \(m\)，其围绕球形天体质量为 \(M\)，探测器与天体中心之间距离为 \(r\)，探测器相比天体很小，可认为是质点。

如图 1 所示，以天体中心为坐标原点，建立极坐标系 \((r, \; \theta)\)，其极轴方向假定任意，极角逆时针旋转方向为正，沿极径与极角方向的单位矢量分别为 \(\vec{e_{r}}\) 与 \(\vec{e_{\theta}}\)。现推导其在天体引力下的运动轨道方程 \(r = f(\theta)\)。

图 1 探测器绕天体运动示意图

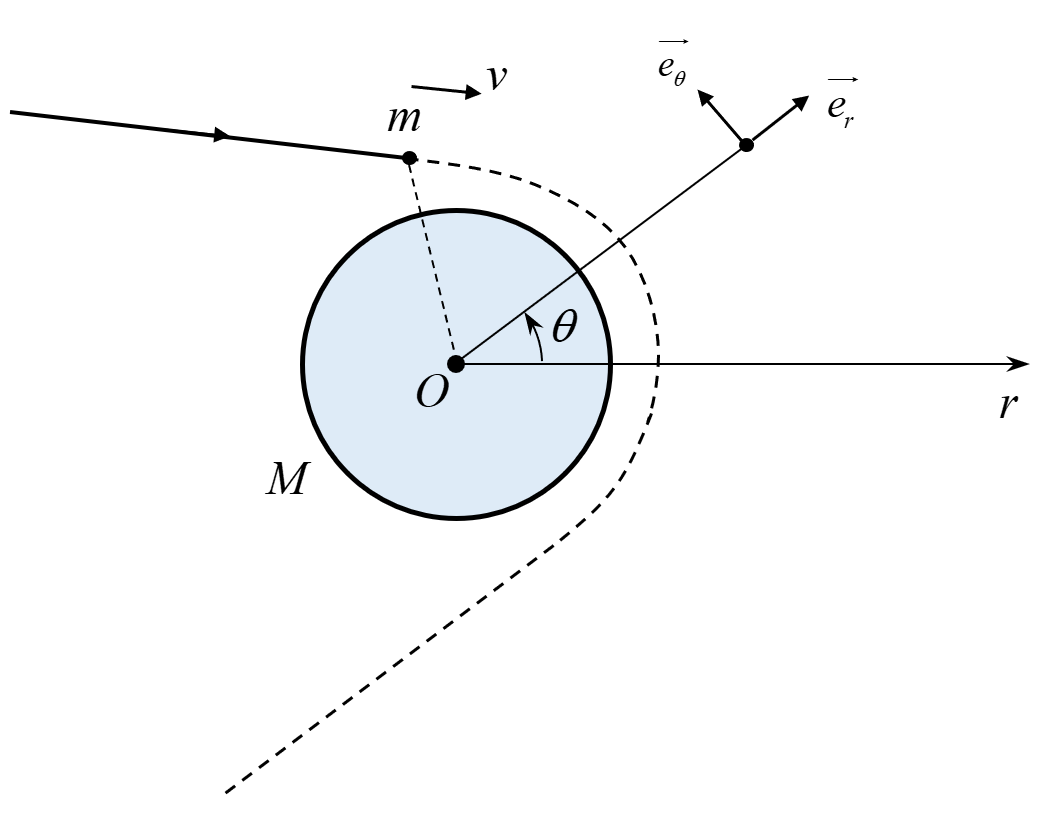
下面推导探测器所受加速度 \(\vec{a}\) 的矢量表达式。探测器的位置矢量 \(\vec{r}\) 可表示为 \[ \vec{r} = r \vec{e_{r}} \tag{1} \label{1} \] 注意到，固定极径 \(r\) 改变极角 \(\theta\) 时， \(\vec{e_{r}}\) 变化；而固定极角 \(\theta\) 改变极径 \(r\) 时，\(\vec{e_{r}}\) 不变，故上式中 \(\vec{e_{r}}\) 仅为 \(\theta\) 的函数，即 \(\vec{e_{r}} = \vec{e_{r}}(\theta)\)，类似可得 \(\vec{e_{\theta}} = \vec{e_{\theta}}(\theta)\)。

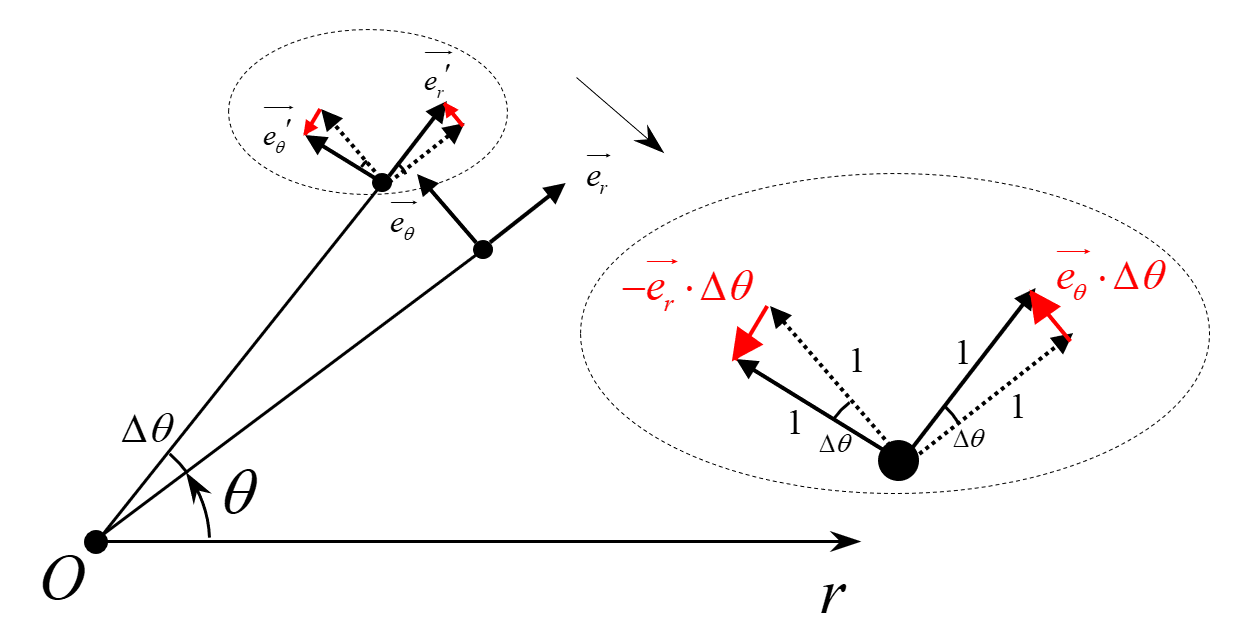
首先，给出后续推导过程中涉及到的几个矢量关系式。如图 2 所示，由导数与矢量几何性质，容易证明以下两个关系式成立 \[ \frac{\mathrm{d} \vec{e_{r}}}{\mathrm{d} \theta} = \lim_{\Delta \theta \to 0} \frac{\left.\vec{e}_{r}\right|_{\theta + \Delta \theta} - \left.\vec{e}_{r}\right|_{\theta}}{\Delta \theta} = \vec{e_{\theta}} \tag{2} \label{2} \]

\[ \frac{\mathrm{d} \vec{e_{\theta}}}{\mathrm{d} \theta} = \lim_{\Delta \theta \to 0} \frac{\left.\vec{e}_{\theta}\right|_{\theta + \Delta \theta} - \left.\vec{e}_{\theta}\right|_{\theta}}{\Delta \theta} = - \vec{e_{r}} \tag{3} \label{3} \]

图 2 矢量关系式推导示意图

由求导及链式法则，可得探测器的速度矢量 \(\vec{v}\) 为 \[ \vec{v} = \frac{\mathrm{d} \vec{r}}{\mathrm{d} t} = \dot{r} \vec{e_{r}} + r \frac{\mathrm{d} \vec{e_{r}}}{\mathrm{d} t} = \dot{r} \vec{e_{r}} + r \frac{\mathrm{d} \vec{e_{r}}}{\mathrm{d} \theta} \dot{\theta} \tag{4} \label{4} \] 上式中简写符号 \(\dot{x}\) 表示将变量 \(x\) 对时间 \(t\) 求导。将式 \(\eqref{2}\) 代入式 \(\eqref{4}\) 可得 \[ \vec{v} = \dot{r} \vec{e_{r}} + r \dot{\theta} \vec{e_{\theta}} \tag{5} \label{5} \] 进一步，将上式 \(\eqref{5}\) 两边对时间 \(t\) 再求一次导数，代入关系式 \(\eqref{2}\) \(\eqref{3}\)，可得加速度矢量表达式为 \[ \begin{aligned} \vec{a}=\frac{\mathrm{d} \vec{v}}{\mathrm{~d} t} & = \frac{\mathrm{d}}{\mathrm{d} t} \left(\dot{r} \vec{e}_{r}\right) + \frac{\mathrm{d}}{\mathrm{d} t}\left(r \dot{\theta} \vec{e}_{\theta}\right) \\ & = \ddot{r} \vec{e}_{r}+\dot{r} \frac{\mathrm{d} \vec{e}_{r}}{\mathrm{~d} t} + \dot{r} \dot{\theta} \vec{e}_{\theta} + r \ddot{\theta} \overrightarrow{e_{\theta}} + r \dot{\theta} \frac{\mathrm{d} \vec{e}_{\theta}}{\mathrm{d} t} \\ & = \ddot{r} \vec{e}_{r} + \dot{r} \dot{\theta} \vec{e_{\theta}} + \dot{r} \dot{\theta} \vec{e_{\theta}} + r \ddot{\theta} \vec{e_{\theta}} - r \dot{\theta}^{2} \vec{r_{r}} \\ & = \left(\ddot{r} - r \dot{\theta}^2\right) \vec{e_{r}} + \left(2 \dot{r} \dot{\theta} + r \ddot{\theta}\right) \vec{e_{\theta}} \end{aligned} \tag{6} \label{6} \] 由于探测器所受天体的万有引力提供其全部加速度，故由牛顿第二定律可列出方程 \[ \vec{F} = m \vec{a} \tag{7} \label{7} \] 根据万有引力定律 \[ \vec{F} = - \frac{G M m}{r^{2}} \vec{e_{r}} \tag{8} \label{8} \] 其中，\(G\) 为引力常量。联立式 \(\eqref{7}\) \(\eqref{8}\)，并将式 \(\eqref{6}\) 代入，可得 \[ - \frac{G M m}{r^{2}} \vec{e_{r}} = m \left[\left(\ddot{r} - r \dot{\theta}^2\right) \vec{e_{r}} + \left(2 \dot{r} \dot{\theta} + r \ddot{\theta}\right) \vec{e_{\theta}}\right] \tag{9} \label{9} \] 整理可得 \[ m \left[\left(\ddot{r} - r \dot{\theta}^2\right) + \frac{G M}{r^{2}}\right] \vec{e_{r}} + m \left(2 \dot{r} \dot{\theta} + r \ddot{\theta}\right) \vec{e_{\theta}} = \vec{0} \tag{10} \label{10} \] 由单位矢量 \(\vec{e_{r}}\) 与 \(\vec{e_{\theta}}\) 的正交性，可得以下方程组 \[ \begin{align} &\left(\ddot{r} - r \dot{\theta}^2\right) + \frac{G M}{r^{2}} = 0 \quad \tag{11} \label{11}\\ &\left(2 \dot{r} \dot{\theta} + r \ddot{\theta}\right) = 0 \quad \tag{12} \label{12} \end{align} \] 观察上述方程组，其中出现 \(r\) 与 \(\theta\) 对时间 \(t\) 的各阶导数，而轨道方程与时间应无关，故考虑将关于时间的导数项转换为 \(r\) 与 \(\theta\) 之间的关系式。

将式 \(\eqref{12}\) 两边同乘 \(r\) ，左边化为全微分，则方程可改写为 \[ \frac{\mathrm{d}}{\mathrm{d} t} \left(r^{2} \dot{\theta}\right) = 2 r \dot{r} \dot{\theta} + r^{2} \ddot{\theta} = 0 \tag{13} \label{13} \] 则解得 \[ r^{2} \dot{\theta} = L = \operatorname{const}. \tag{14} \label{14} \] 由此可知，在探测器绕天体运行过程中，\(r^{2} \dot{\theta}\) 为一守恒量，被称为第一守恒量，采用 \(L\) 表示，实际上它是物体在有心力运动下角动量守恒的数学体现。

根据式 \(\eqref{14}\)，可得 \[ \dot{\theta} = \frac{L}{r^{2}} \tag{15} \label{15} \] 将上式 \(\eqref{15}\) 代入式 \(\eqref{11}\)，整理可得 \[ \ddot{r} - r \left(\frac{L}{r^{2}}\right)^{2} + \frac{G M}{r^{2}} = 0 \tag{16} \label{16} \] 由上式可得根据守恒量，可以消去 \(\theta\) 关于时间 \(t\) 的导数，下面尝试消去 \(r\) 关于时间 \(t\) 的导数。由链式法则可得 \[ \dot{r} = \frac{\mathrm{d} r}{\mathrm{d} t} = \frac{\mathrm{d} r}{\mathrm{d} \theta} \dot{\theta} = r_{\theta} \cdot \frac{L}{r^{2}} \tag{17} \label{17} \] 上式中，\(r_{\theta}\) 代表变量 \(r\) 对变量 \(\theta\) 求导。再将上式两边对时间 \(t\) 求导一次，可得 \[ \ddot{r} = \frac{\mathrm{d} \dot{r}}{\mathrm{d} t} = \frac{\mathrm{d}}{\mathrm{d} t} \left(r_{\theta} \frac{L}{r^{2}}\right) = \frac{\mathrm{d}}{\mathrm{d} \theta} \left(r_{\theta} \cdot \frac{L}{r^{2}}\right) \dot{\theta} = \frac{\mathrm{d}}{\mathrm{d} \theta} \left(r_{\theta} \cdot \frac{L}{r^{2}}\right) \cdot \frac{L}{r^{2}} \tag{18} \label{18} \] 将上式 \(\eqref{18}\) 代入式 \(\eqref{16}\) 可得 \[ \frac{\mathrm{d}}{\mathrm{d} \theta} \left(r_{\theta} \cdot \frac{L}{r^{2}}\right) \cdot \frac{L}{r^{2}} - r \left(\frac{L}{r^{2}}\right)^{2} + \frac{G M}{r^{2}} = 0 \tag{19} \label{19} \] 将上式两边同乘 \(r^{2} / L\)，化简可得 \[ \frac{\mathrm{d}}{\mathrm{d} \theta} \left(r_{\theta} \cdot \frac{\mathrm{d}}{\mathrm{d} r} \left(\frac{L}{r}\right)\right) + r \cdot \left(\frac{L}{r^{2}}\right) = \frac{G M}{L} \tag{20} \label{20} \] 进一步整理可得 \[ \frac{\mathrm{d}^{2}}{\mathrm{d} \theta^{2}} \left(\frac{L}{r}\right) + \left(\frac{L}{r}\right) = \frac{G M}{L} \tag{21} \label{21} \] 上式可视为变量 \((L/r)\) 关于自变量 \(\theta\) 的二阶非齐次线性微分方程，其解为齐次微分方程通解与原方程某特解的叠加，具体求解过程从略。得到最终解为 \[ \frac{L}{r} = A \cos(\theta + \psi) + \frac{G M}{L} \tag{22} \label{22} \] 其中，\(A,\;\psi\) 为待定系数。将上式 \(\eqref{22}\) 变形，可得 \[ r = \frac{\frac{L^{2}}{G M}}{1 + \frac{L A}{G M} \cos(\theta + \psi)} \tag{23} \label{23} \] 上式即为探测器的轨道方程，其形式为极坐标系下的圆锥曲线，但其中仍包含未知系数。下面引入条件来确定待定常数 \(A,\;\psi\)，进一步化简轨道方程。

• 条件 1：假设选择极轴（即 \(\theta = 0\) 的径矢）穿过探测器关于天体的近地点，确定 \(\psi\)。

如图 3 所示，由天体运动物理知识可知，近地点为探测器轨道曲率半径最小的位置，其值设为 \(r_{\min}\)。

图 3 选择极轴穿过近地点情况下探测器绕天体运动示意图

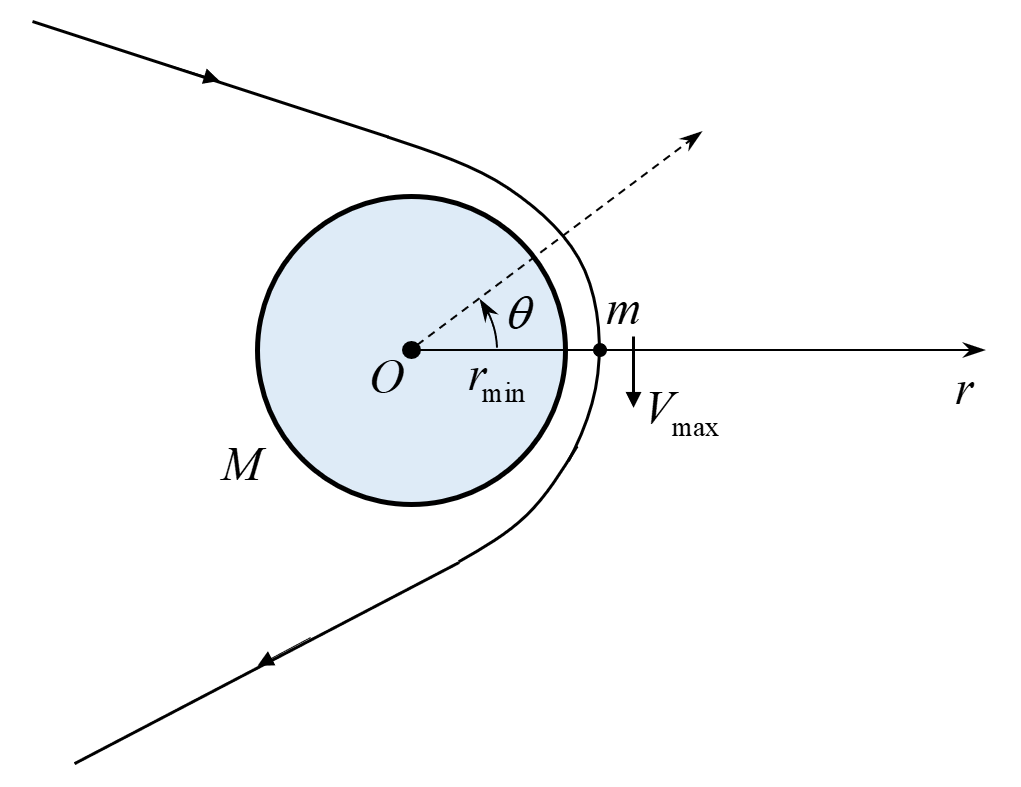
若当 \(\theta = 0\) 时，有 \(r = r_{\min}\)，则须满足轨道方程分母中，\(\cos(\theta + \psi)\) 取得极大值，故在一个周期 \([0, 2 \pi)\) 内，当且仅当 \(\psi = 0\) 时，满足条件，此时有 \[ r_{\min} = \frac{\frac{L^{2}}{G M}}{1 + \frac{L A}{G M}} \tag{24} \label{24} \]

• 条件 2：假设给定探测器的总能量为 \(E_{0}\)，由能量守恒关系确定 \(A\)。

在满足条件 1 的约束下，考虑条件 2。

一方面，探测器在近地点满足 \(r = r_{\min}\)，且其运行速度达到最大值 \(V = V_{\max}\)，且满足速度为轨道切向，法向分量为零，即 \(V = V_{\tau}\)。

另一方面，考虑式 \(\eqref{14}\) 角动量守恒量，在近地点满足以下关系

\[ r^{2} \dot{\theta} = r \cdot \left(r \dot{\theta}\right) = r \cdot V_{\tau} = r_{\min} \cdot V_{\max} = L \tag{25} \label{25} \]

故由上式 \(\eqref{25}\) 可得关系式 \[ V_{\max} = \frac{L}{r_{\min}} \tag{26} \label{26} \] 探测器的总能量 \(E_{0}\) 由动能与势能组成，在近地点有以下守恒方程成立 \[ E_{0} = \frac{1}{2} m V_{\max}^{2} - \frac{G M m}{r_{\min}} = \frac{1}{2} m \cdot \frac{L^{2}}{r_{\min}^{2}} - \frac{G M m}{r_{\min}} \tag{27} \label{27} \] 联立式 \(\eqref{24}\) \(\eqref{27}\)，可解得 \[ A = \frac{G M}{L} \sqrt{1 + \frac{2 E_{0} L^{2}}{G^{2} M^{2}}} \tag{28} \label{28} \] 故通过引入以上两个条件，已经确定出待定系数 \(A,\;\psi\)，将其代入式 \(\eqref{23}\) 可得 \[ r = \frac{\frac{L^{2}}{G M}}{1 + \sqrt{1 + \frac{2 E_{0} L^{2}}{G^{2} M^{2}}} \cos \theta} \tag{29} \label{29} \] 上式即为考虑极轴穿过近地点且携带总能量 \(E_{0}\) 的探测器绕天体运行的最终轨道方程，其为圆锥曲线形式。

下面对轨道方程 \(\eqref{29}\) 进行分析。定义离心率 \[ e = \sqrt{1 + \frac{2 E_{0} L^{2}}{G^{2} M^{2}}} \tag{30} \label{30} \] 由圆锥曲线知识，不同离心率 \(e\) 情况的轨道形状如下： \[ \left\{\begin{array}{c} e = 0, \quad \quad &\text{Circle} \\ 0 < e < 1, \quad \quad &\text{Ellipse}\\ e = 1, \quad \quad &\text{Parabola (escape)}\\ e > 1, \quad \quad &\text{Hyperbola (escape)} \end{array}\right. \tag{31} \label{31} \] 由式 \(\eqref{30}\) 表达式，可知探测器携带的总能量 \(E_{0}\) 与离心率 \(e\) 之间相关，也即与轨道形状密切相关，分别讨论如下：

• 情形 1：当 \(E_{0} \geqslant 0\) 时，\(e \geqslant 1\)。

此时探测器沿开放轨道将作逃逸运动，不会被天体捕获。该情形对应最小能量为 \(E_{0} = 0\)，轨道为抛物线（Parabola），结合式 \(\eqref{27}\) 可解得 \(V_{\max}\)，此为探测器绕天体运行的最小逃逸速度。对于地球，可计算该速度为 \[ V_{\max} = \sqrt{\frac{2 G M}{r_{\min}}} = \sqrt{\frac{2 \times 6.67 \times 10^{-11} \times 5.97 \times 10^{24}}{6.38 \times 10^{6}}} \approx 11.2 \; \text{km/s} \tag{32} \label{32} \] 此也即探测器脱离地球引力控制所需的第二宇宙速度。

• 情形 2：当 $ - (G M m)/(2 r) E_{0} < 0$ 时，\(0 \leqslant e < 1\)。

此时探测器沿椭圆轨道，围绕绕天体作周期性运动，被天体捕获。若 \(E_{0} = -(G M m)/(2 r)\)，则 \(e = 0\)，轨道为圆（Circle），结合式 \(\eqref{27}\) \(\eqref{29}\) 可解得 \(V_{\max}\)，此为探测器绕天体周期运动的最小围绕速度。对于地球，可计算该速度为 \[ V_{\max} = \sqrt{\frac{G M}{r_{\min}}} = \sqrt{\frac{6.67 \times 10^{-11} \times 5.97 \times 10^{24}}{6.38 \times 10^{6}}} \approx 7.9 \; \text{km/s} \tag{33} \label{33} \] 此也即探测器围绕地球旋转所需的第一宇宙速度。

• 情形 3：当 \(E_{0} < - (G M m)/(2 r)\) 时，\(e < 0\)。

此时，探测器的总能量无法将探测器加速至天体的第一宇宙速度，探测器将返回天体表面（crash to earth）而失效。

另外，还可以在拉格朗日（Lagrangrian）或者哈密顿（Hamiltonian）力学框架下以更精练的方法对方程进行推导。

值得一提的是，Hamiltonian 力学框架是量子力学的奠基石。

---

^_^ This is the END of the article. Thank you for reading!

If you think this article is helpful to you, do not hesitate to leave your comments!

Finished by pkufzh (Small Shrimp) on 2022/03/10 .

Who am I? A happy shrimp from Peking University!